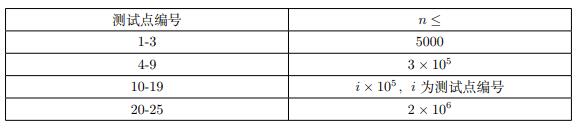
基础分治练习题
1.1 题目描述
这是一道基础分治练习题。 给你三个数列 {ai}, {bi}, {ci},保证每个数列都恰好是一个排列。你需要求出满足 ai < aj , bi < bj , ci < cj 的有序对 (i, j) 的数目。
1.2 输入格式
从文件 cdq.in 中读入数据。 数据的第一行包含一个正整数 n,表示数列的长度。接下来一行三个非负整数 SA, SB, SC。 为了避免过量的输入对程序的运行效率产生影响,{ai}, {bi}, {ci} 由以下代码生成:
const int N = 2e6+5;
unsigned int SA,SB,SC;int n,a[N],b[N],c[N];
unsigned int rd()
{
SA^=SA<<16;SA^=SA>>5;SA^=SA<<1;
unsigned int t=SA;SA=SB;SB=SC;SC^=t^SA;return SC;
}
void gen(int *P)
{
for (int i=1;i<=n;++i) P[i]=i;
for (int i=1;i<=n;++i) swap(P[i],P[1+rd()%n]);
}
int main()
{
scanf("%d%u%u%u",&n,&SA,&SB,&SC);
gen(a);gen(b);gen(c);return 0;
}你可以在程序中自由运行这段代码。在下发文件中提供了这段代码的 cpp 文件,你可以选择直接在 该 cpp 文件下编写程序,也可以假装看不见它。
1.3 输出格式
输出到文件 cdq.out 中。 输出一行一个正整数 ans,表示满足条件的有序对 (i, j) 的对数。
1.4 样例 1 输入
5
233 666 667
1.5 样例 1 输出
4
1.6 样例 1 解释
生成的数列为 a = {1, 2, 3, 4, 5}, b = {1, 5, 3, 2, 4}, c = {3, 4, 2, 1, 5}。 显然有且仅有 (1, 2),(1, 5),(3, 5),(4, 5) 这四个数对满足条件。
1.7 样例 2 输入
100000
123 456 789
1.8 样例 2 输出
1258889897
1.9 子任务
对于 100% 的数据,保证 1 ≤ n ≤ 2 × 106, 1 ≤ SA, SB, SC ≤ 109。
请注意常数因子对程序运行效率带来的影响。
1.10 提示
加油!这是道水题!A 掉它
看到这道题的第一眼就是cdq分治。敲开心。然后。。。

总之,只要你常数足够优秀(大概八分之一),就可以用cdqA掉此题
然后我们来看看这道神仙题到底在干什么。
根据1.2给出的输入生成程序,我们能一眼看出生成的三个数列其实并木有重复的元素,而且都小于等于n。也就是说,,这三个数列其实都是1~n的排列。
然后我们看看数据范围:2e6,只有O(n)和O(nlogn)两种实际意义的复杂度可以过。那么,我们能想到什么呢?二维偏序是nlogn的。所以,我们可以尝试将题目转成求二维偏序。
我们来看下面这三个东西:
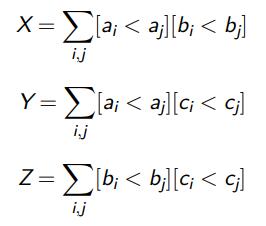
明显,对于符合要求的数对,一定会在X,Y,Z中各别计算一次,而对于不符合要求的,只会在X,Y,Z中的一个里被计算一次。那么,我们可以得出:
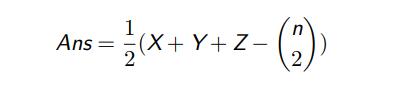
这样,这道题就解决了。(然而我并不知道为什么我一个log还没有两个log快。。。)
1 |
|
请自动忽视头文件里的乱码以及代码奇怪的高亮