左偏树(Leftist Tree)是一种可并堆的实现。

左偏树相比于有两个额外的属性：键值和距离。 键值 是用于比较节点的大小。 距离 则是如下定义的： 节点i称为外节点(external node)，当且仅当节点i的左子树或右子树为空(left(i)=NULL或right(i)=NULL)。 节点i的距离(dist(i))是节点i到它的后代中，最近的外节点所经过的边数。 特别的，如果节点i本身是外节点，则它的距离为0；而空节点的距离规定为-1 (dist(NULL)=-1)。

左偏树满足下面两条基本性质：

[性质1] 节点的键值小于或等于它的左右子节点的键值。即key(i)≤key(parent(i))

[性质2] 节点的左子节点的距离不小于右子节点的距离。即dist(left(i))≥dist(right(i))

这两条性质是对每一个节点而言的，因此可以简单地从中得出，左偏树的左右子树都是左偏树。 由这两条性质，我们可以得出左偏树的定义：左偏树是具有左偏性质的堆有序二叉树。

下图是一棵左偏树：

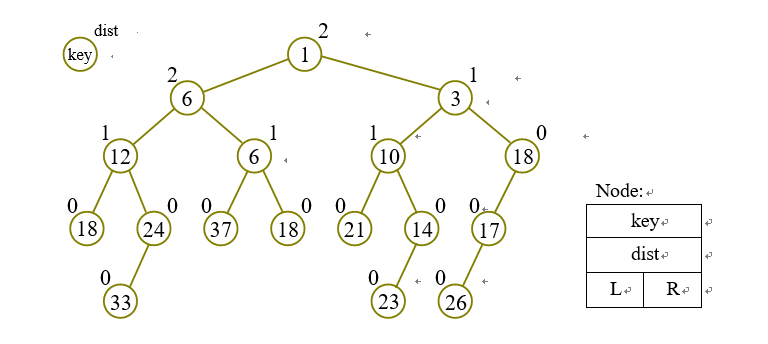
[性质3] 节点的距离等于它的右子节点的距离加1。即dist(i)=dist(right(i))+1。

左偏树并不是为了快速访问所有的节点而设计的，它的目的是快速访问最小节点以及在对树修改后快速的恢复堆性质。 从图中我们可以看到它并不平衡，由于性质2的缘故，它的结构偏向左侧，不过距离的概念和树的深度并不同，左偏树并不意味着 左子树的节点数或是深度一定大于右子树。

下面我们来讨论左偏树的距离和节点数的关系。

[引理1] 若左偏树的距离为一定值，则节点数最少的左偏树是完全二叉树。 证明：由性质2可知，当且仅当对于一棵左偏树中的每个节点i，都有dist(left(i))=dist(right(i))时，该左偏树的节点数最少。显然具有这样性质的二叉树是完全二叉树。

[定理1] 若一棵左偏树的距离为k，则这棵左偏树至少有2^(k+1)-1个节点。 证明：由引理1可知，当这样的左偏树节点数最少的时候，是一棵完全二叉树。距离为k的完全二叉树高度也为k，节点数为2^(k+1)-1，所以距离为k的左偏树至少有2k＋1-1个节点。

作为定理1的推论，我们有：

[性质4] 一棵N个节点的左偏树距离最多为O(log(N+1)-1)。

有了上面的4个性质，我们可以开始讨论左偏树的操作了。

左偏树的合并

C ← Merge(A,B) 把A,B两棵左偏树合并，返回一棵新的左偏树C，包含A和B中的所有元素。在本文中，一棵左偏树用它的根节点的指针表示。

在合并操作中，最简单的情况是其中一棵树为空（也就是，该树根节点指针为NULL）。这时我们只须要返回另一棵树。

若A和B都非空，我们假设A的根节点小于等于B的根节点（否则交换A,B），把A的根节点作为新树C的根节点，剩下的事就是合并A的右子树right(A)和B了。

right(A) ← Merge(right(A),B)

为了维护左偏性质，若dist(left(A))>dist(right(A))，交换left(A)和right(A)。

最后，由于right(A) 的距离可能发生改变，我们必须更新A的距离： dist(A) ← dist(right(A)) + 1

于是合并就完成了。

下图是一个合并过程的示例：

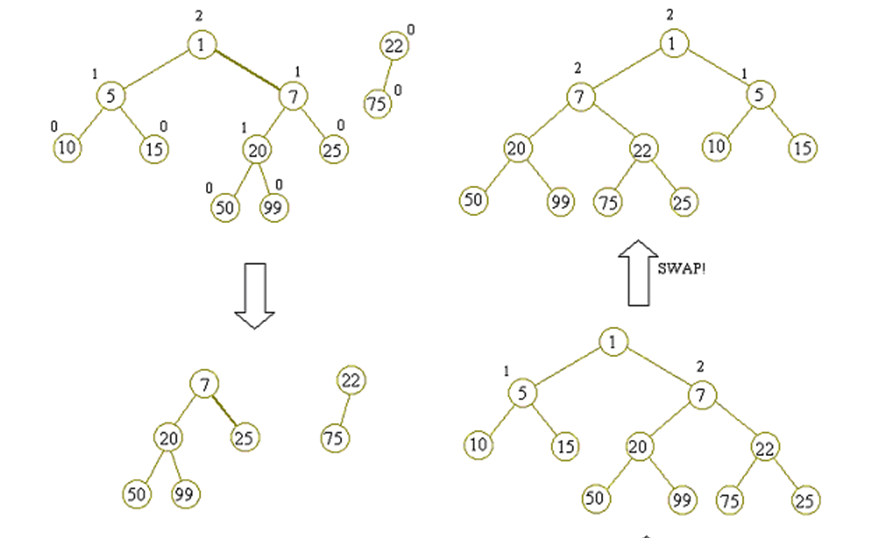
插入新节点

单节点的树一定是左偏树，因此向左偏树插入一个节点可以看作是对两棵左偏树的合并。

由于合并的其中一棵树只有一个节点，因此插入新节点操作的时间复杂度是O(logn)。

删除最小节点

由性质1，我们知道，左偏树的根节点是最小节点。在删除根节点后，剩下的两棵子树都是左偏树，需要把他们合并。

由于删除最小节点后只需进行一次合并，因此删除最小节点的时间复杂度也为O(logn)。

左偏树的构建

将n个节点构建成一棵左偏树，这也是一个常用的操作。

算法一 暴力算法——逐个节点插入，时间复杂度为O(nlogn)。

算法二 仿照二叉堆的构建算法，我们可以得到下面这种算法：  将n个节点（每个节点作为一棵左偏树）放入先进先出队列。不断地从队首取出两棵左偏树，将它们合并之后加入队尾。当队列中只剩下一棵左偏树时，算法结束，时间复杂度为O(n)。

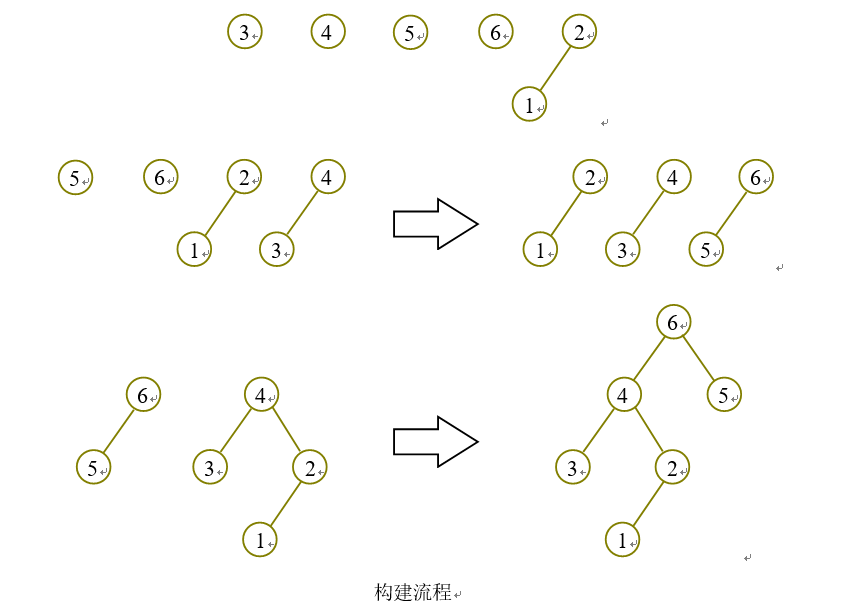
代码如下：

#include <algorithm> //STL通用算法
#include <cmath> //定义数学函数
#include <cstdio> //定义输入/输出函数
#include <iostream> //数据流输入/输出
#include <cstring> //字符串处理
#include <string> //字符串类
#include <ctime> //定义关于时间的函数
#define itn int
#define fro for
#define ll long long
#define reg register
#define inf 1234567890
/*#include <bitset> //STL位集容器
#include <cstype> //字符处理
#include <cerrno> //定义错误码
#include <complex> //复数类
#include <clocale> //定义本地化函数
#include <cstdlib> //定义杂项函数及内存分配函数
#include <deque> //STL双端队列容器
#include <exception> //异常处理类
#include <fstream> //文件输入/输出
#include <functional> //STL定义运算函数(代替运算符)
#include <limits> //定义各种数据类型最值常量
#include <list> //STL线性列表容器
#include <map> //STL映射容器
#include <iomanip> //参数化输入/输出
#include <ios> //基本输入/输出支持
#include <iosfwd> //输入/输出系统使用的前置声明
#include <istream> //基本输入流
#include <ostream> //基本输出流
#include <queue> //STL队列容器
#include <set> //STL集合容器
#include <sstream> //基于字符串的流
#include <stack> //STL堆栈容器
#include <stdexcept> //标准异常类
#include <streambuf> //底层输入/输出支持
#include <utility> //STL通用模板类
#include <vector> //STL动态数组容器
#include <cwchar.h>//宽字符处理及输入/输出
#include <cwctype.h> //宽字符分类*/

using namespace std;

int ans;

int max(int x,int y){return x>y?x:y;}

int min(int x,int y){return x<y?x:y;}

void swap(int &x,int &y){int d=x;x=y;y=d;}

int read()
{
    int x=0,f=1;char ch=getchar();
    while (ch<'0' || ch>'9'){if (ch=='-')f=-1;ch=getchar();}
    while ('0'<=ch && ch<='9'){x=x*10+(ch^48);ch=getchar();}
    return x*f;
}

void write(int x)
{
    int buf[50];
    if (x<0) putchar('-'),x=-x;
    buf[0]=0;
    while (x) buf[++buf[0]]=x%10,x/=10; 
    if (!buf[0]) buf[0]=1,buf[1]=0;
    while (buf[0]) putchar('0'+buf[buf[0]--]);
}

int fa[100100],dist[100100],Left[100100],Right[100100],key[100100];

int find(int x)
{
    return fa[x]?find(fa[x]):x;
}

int merge(int x,int y)
{
    if (x==0) return y;
    if (y==0) return x;
    if (key[y]<key[x]||(key[x]==key[y]&&x>y)) swap(x,y);
    int &l=Left[x],&r=Right[x];
    r=merge(r,y);
    fa[r]=x;
    if (dist[r]>dist[l]) swap(l,r);
    dist[x]=dist[r]+1;
}

void Delete(int x)
{
    key[x]=-1;
    fa[Right[x]]=fa[Left[x]]=0;
    merge(Left[x],Right[x]);
}

int main(){
    int n=read(),m=read();
    dist[0]=-1;
    for (int i=1;i<=n;i++) key[i]=read();
    while (233333&&m--)
    {
        int q=read();
        if (q==1)
        {
            int x=read(),y=read();
            if (key[x]==-1||key[y]==-1) continue;
            x=find(x),y=find(y);
            if (x!=y) merge(x,y);
        }
        if (q==2)
        {
            int x=read();
            if (key[x]==-1) printf("-1\n");
            else 
            {
                x=find(x);
                printf("%d\n",key[x]);
                Delete(x);
            }
        }
    }
    return 0;
}